The Segregation Model | Variations on the Basic Segregation Model | A Polygon Model of Segregation
- Source Code for segModelPolygonRandom (195 KB)
- Source Code for segModelPolygon (191 KB)
- Shapefile (1.48 MB )
All the models up to this point have focused on agents moving within the environment in which they are located. What has become noticeable is the importance of space, especially the development of empty space when segregation emerges. This model (see segModelPolygonRandom model for further details) moves away from representing agents as points, to representing them as polygons, such as building outlines or groups of individuals aggregated into wards. The aim of this model is to explore the importance of empty space on the pattern of segregation that emerges.
As with previous models, this extends the basic model. However, instead of creating point agents of different types based on population fields held within the data file of the shapefile, polygon agents are created. While this is done randomly, agents can be created based on the dominant social group of the area held within the data file if required (see segModelPolygon for an example). Within the model, two types of agents are created either of type red or blue, while a certain percentage of area remains unoccupied (black, see the buildModel Method in SegGISModelRandom). Each polygon knows which other polygons share a common edge to it. These neighbourhoods are stored within the .GAL file (see Polygon Agents in Basic Model or for a worked example see testNeighbours and setNeighbors in UrbanAgent Class). Figure 1 demonstrates how different polygons have different numbers of neighbours, with areas that are separated by geographical features such as rivers are not considered as neighbours.
What drives the model is neighbourhood composition, and as with the basic segregation model, agents want to live in an area where a certain percentage of their neighbours are of the same type as themselves. This is calculated using the neighbours that share a common edge to the agent in question (Figure 2). If an agent is dissatisfied with its current neighbourhood (calculated in evaluateAndSetHappiness method in the UrbanAgent class), it will move to a random empty polygon, regardless of whether or not this new location meets its preference (see move method in the UrbanAgent class). This was done to force the agents to move. For example, if the agents only moved to areas where their preferences could be matched and where there were no areas where this could be achieved, the system would not evolve, as unlike in the basic segregation model, agents are not removed. Each time an agent moves from an occupied to an unoccupied area, a counter is updated for the area where the agent has just moved to, therefore allowing one to study how often agents move throughout the course of a simulation (see numberOfTimeChanged field in the UrbanAgent class).
Figure 1: A selection of polygons and their polygon neighbours selected.
Figure 2: Pseudo-code for blue agents evaluating their neighbourhood.
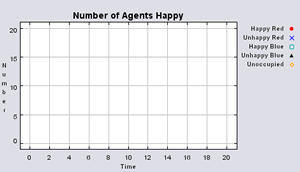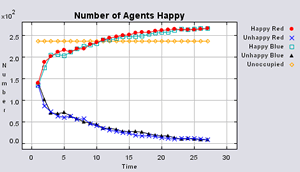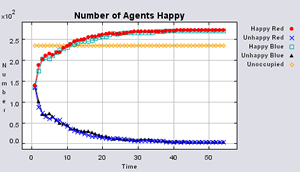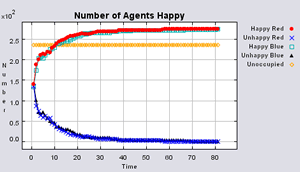
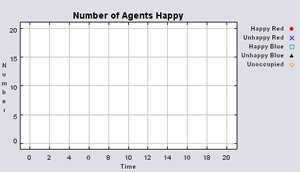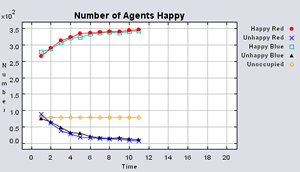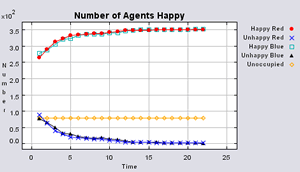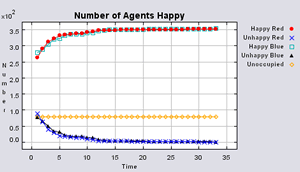
The following scenarios will explore how different degrees of empty space affect the outcome of the model ranging from 40% to 10% unoccupied space. In order for agents to move, there needs to be some vacant space. To avoid studying the effects of restricted movement, Schelling (1971) suggests 25-30% vacancy to allow for fair freedom of movement. Within all simulations, agents want to be in areas where 50% or more of their neighbours are of the same type as themselves.
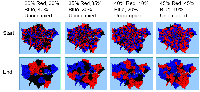
Figure 3 highlights the typical patterns of segregation that arise from different ratios of red, blue and unoccupied (black) space within the simulations. One can clearly see the effect of geographical features on the outcome of the pattern of segregation (i.e. the river Thames in this example) and Table 1 highlights the average results from multiple model runs of the polygon model. In each case, there are a number of areas which did not change state. Animations for different compositions of red and blue agents and unoccupied space highlighting how the system segregates based on images from Figure 3 can be seen below.
Table 1 additionally highlights the effect the amount of empty space plays on the number of iterations until all agents are satisfied (In some instances, if the tolerances are set too high and there is not enough free space, the model does not stabilise. However this only occurred occasionally). The less empty space, the less number of iterations it takes on average for all agents to become satisfied. However, this also relates to the agents’ random movement, for unlike in the previous models, agents move to any empty space, with no consideration if it is a suitable area unlike in the basic segregation model. This has an effect on the outcome of the model. For example, comparing the average number of iterations when 99% of the population are satisfied to the average number of iterations when all the agents are satisfied, clearly increases when there is a greater amount of unoccupied space. Combined with the number of state changes (i.e. changing from unoccupied to occupied) during the course of a simulation, one can clearly see the effect unoccupied space has on the outcome of the model.
Before moving onto the next model, it is felt important to note how visualisation of the segregation outcome is clearer using polygons than when using point agents. However, one assumes all change occurs at the boundary of these polygons while using point agents, but this is not the case as clusters of different types of agents can cross these boundaries.
Figure 3: Typical patterns of segregation with different compositions of red and blue agents and unoccupied space.
Table 1: Average results from running the polygon segregation model.
Animations for different compositions of red and blue agents and unoccupied space highlighting how the system segregates based on images from Figure 3
References
Schelling, T.C. (1971), 'Dynamic Models of Segregation', Journal of Mathematical Sociology 1: 143-186.