The Segregation Model | Models within Paper | The Influence of Geographical Features


 

Areas within cities are bounded by features such as highways, railway lines, rivers, lakes, and parks which can act as boundaries between residential groups.  For example, Rabin (1987) observed that highways formed effective boundaries between the predominant white and minority groups in residential areas in most U.S. cities.  The model was designed to explore the effect these features have on the outcome of a particular simulation (see GIS Operations in the Basic Model).  Thus the segregation model is not only capable of exploring segregation but also examining the effect geographical features have on the pattern of segregation that emerges (i.e. the ability of geographical features to separate neighbourhoods).  The following section will therefore demonstrate how neighbourhoods can be influenced by the geometrical features of the urban environment.  To achieve this, the segregation model will be compared to a variation that does not include geographical features (geometry) when neighbourhoods are being calculated. 

The following section will therefore demonstrate how neighbourhoods can be influenced by the geometrical features of the urban environment.  To achieve this, the basic segregation model will be compared to a variation that does not include geographical features (geometry) when neighbourhoods are being calculated (See segregationModelNoNeighbourhoods model).  Specifically methods that calculate buffers for example, compare the method neighboursWithin methods in the Resident Class from the basic segregation model and segregationModelNoNeighbourhoods model

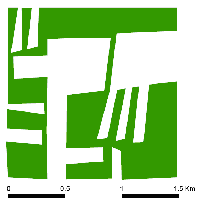
A simple area was used to represent the urban space (Figure 1).  The region was manipulated so that there are areas directly opposite each other but not included in the basic segregation model neighbourhood calculation.  They would only be included for variations of the model where geometry is not considered when calculating neighbourhoods.  The entire area contained 4000 agents (2000 of each type).  Agents within the model have the same preference, and all want to be in an area where 50% or more are of the same type.  Neighbourhood size was set to 200m to account for agents on the fringes of geometrical features. 

Figure 1: The area used to test how geographical features impact on the pattern of segregation.

Figure 2 (and animations of these simulation runs can be seen below) shows a selection of final patterns of segregation from the basic segregation model and the model where geometry was not included.  While the patterns look quite similar suggesting the influence of geometry in neighbourhood calculations is quite subtle.  Where it is most obvious is at the fringes of geometrical boundaries, specifically the top left and centre of the images where agents would consider neighbours on the opposite sides of the spits as neighbours.  This pertains to the cases where geometry was not included in the neighbourhood calculations.  The examination of the summary data presented in Table 1 highlights that the runs which included geometry stabilised more quickly than those without.  However, the mean number of moves and the number times the agents moved are quite similar.  From these simulations, one can see the effect that geometry has on neighbourhood formation which is not normally explicitly included in Schelling-type models.

Figure 2: Screen captures of segregation outputs when all agents are satisfied for different geometrical and non-geometrical models.

Table 1: Comparison of geometrical and non-geometrical models: number of iterations and number of moves until all agents are satisfied.

[TOP]

Animations of simulation runs

 

Geometry included
 

Geometry not included
 
 

[TOP]

Reference

Rabin, Y. (1987), 'The Roots of Segregation in the Eighties: The Role of Local Government Actions', in G.A., Tobin. (ed.) Divided Neighbourhoods: Changing Patterns of Racial Segregation, Sage Publications, London, UK, pp. 208–26.

[TOP]