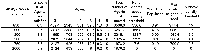The Segregation Model | Variations on the Basic Segregation Model | The Density Model
- Source Code for Segregation Model Density (682 KB)
- Shapefile (5 KB)
The basic segregation model occasionally resulted in agents clustering in small areas while at the same time, leaving other areas relatively unpopulated. This is especially noticeable in the previous model as agents are added and not removed from the system (e.g.run 4 of where agents where only added and not removed). This is the result of not restricting agents to one agent per cell as in many cell space models of segregation.
While areas of high and low population density can be seen in many cities, the question this model asks is what does the final pattern of segregation look like when agents can only move to areas where the population density is below a certain threshold? Thus the following subsection explores how the degree of segregation can be altered by introducing population density limits for neighbourhoods and how this affects the outcome of the model. Density can additionally be considered a proxy for empty space, and an alternative model could be written whereby agents can only move to an area if there are no other agents there as with many cell space agent-based models
This model (Segregation Model Density) varies from the basic segregation model by adding a density threshold into the agent’s preference for a location which is shown in the pseudo-code in Figure 1 (and also see evaluateAndSetHappiness method in Resident Class). Therefore each time an agent evaluates its local neighbourhood or moves to a new area, not only does it calculate the neighbours of each type within a specified distance but it uses the buffered geometry from the neighbourhood calculation to calculate the population density of that area as well (see neighboursWithin method in Resident Class).
Figure 1: Pseudo-code for density rule for an agent to be satisfied.
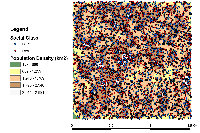
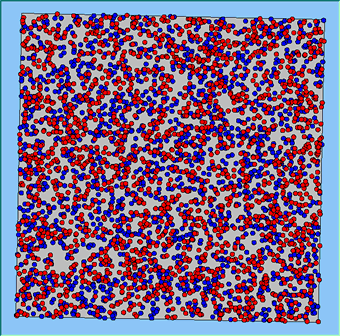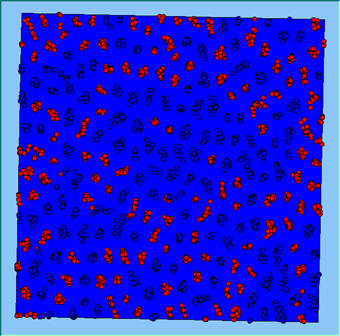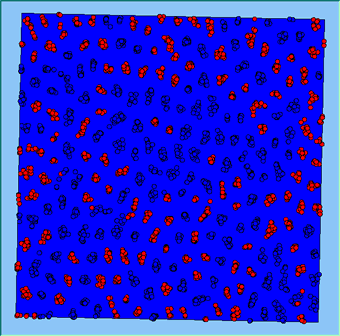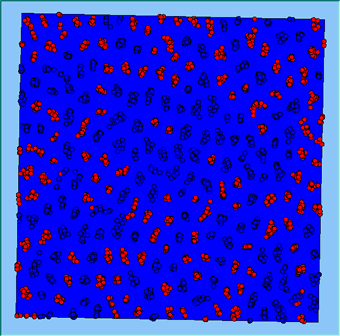
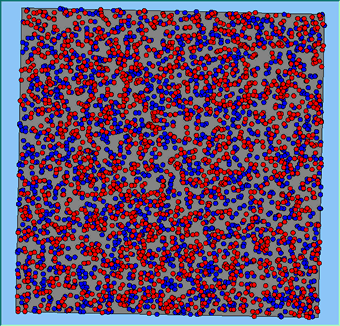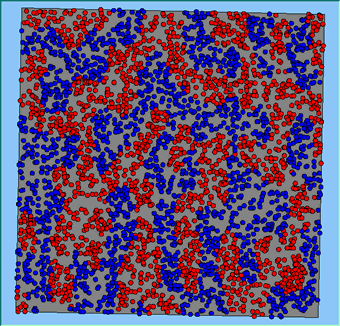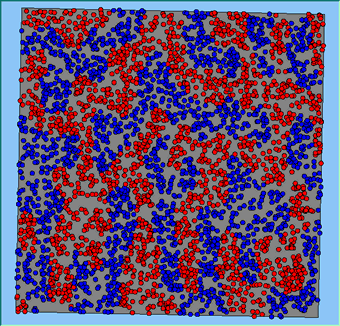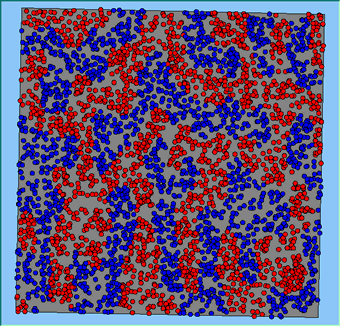
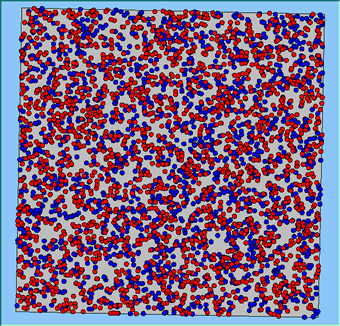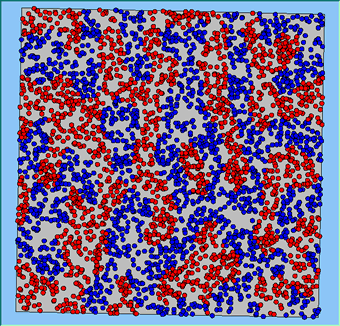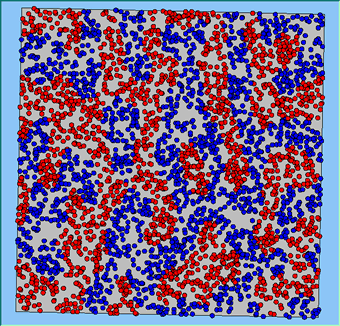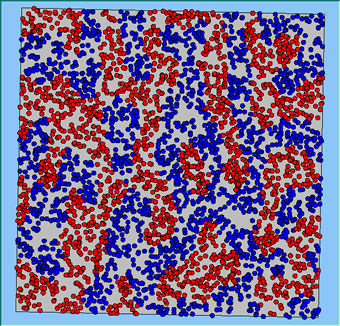
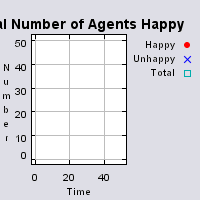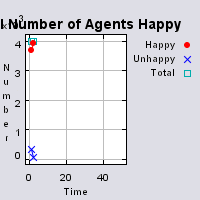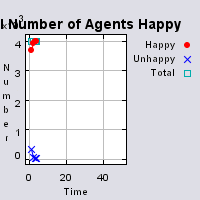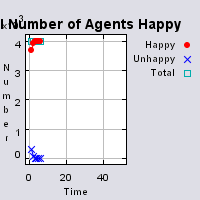
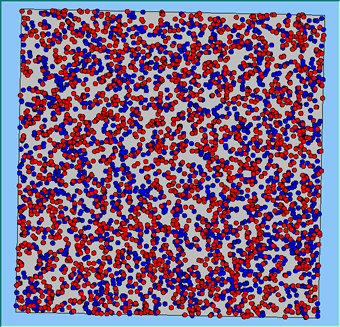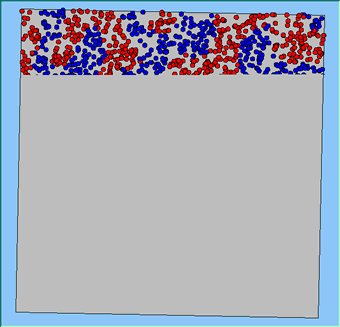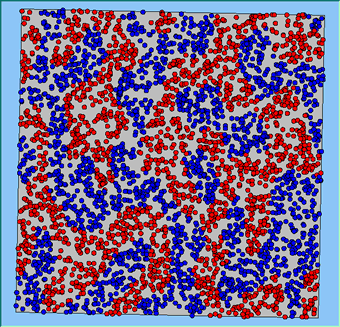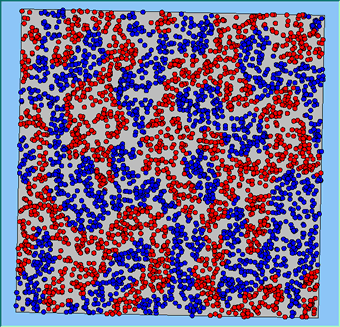
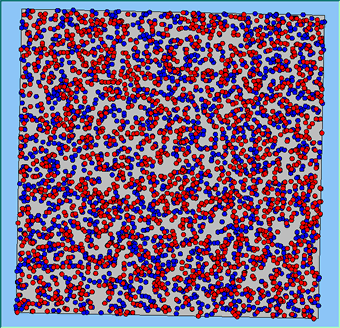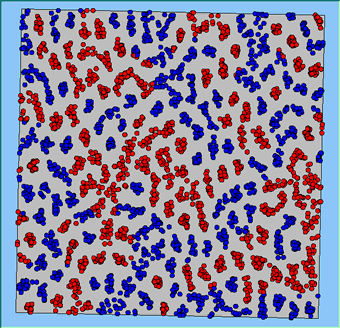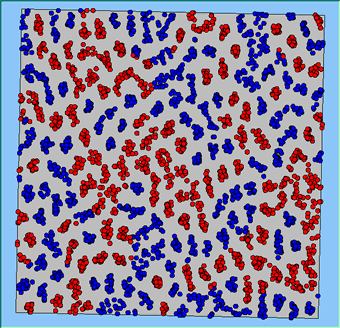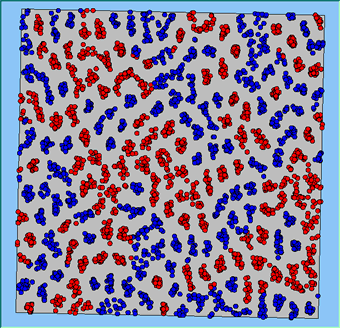
The following analysis will focus on a single area, which contains 4000 agents, with equal numbers of Blues and Reds. The average population density of the area is 1777 people per km2. However within the area, population density varies locally, as can be seen in Figure 2. which shows agents distributed over the area when the model is first initialised and the agents are randomly placed. Calculated using a density function with a search radius of 100m, whereby points that fall within the search area are summed, then divided by the search area size to get each cell’s density value. Larger values of the radius produce a smoother, more generalised density ration. Smaller values produce a raster that shows more detail. For all the simulations, agents want to be in areas where at least 50% of its neighbours are of the same type and neighbourhoods are set at 100m.
The following analysis will focus on a single area which contains 4000 agents with equal numbers of blues and reds. The average population density of the area is 1777 people per km2. However, within the area, population density varies locally, as can be seen in Figure 2 (Calculated using a density function with a search radius of 100m, where points that fall within the search area are summed, then divided by the search area size to get each cell’s density value. Larger values of the radius produce a smoother, more generalised density ratio. Smaller values produce a raster that shows more detail). Figure 2 shows agents distributed over the area when the model is first initialised and the agents are randomly placed. For all the simulations, agents want to be in areas where at least 50% of its neighbours are of the same type and neighbourhoods are set at 100m values.
Figure 2: An example of local population density when the segregation model is first initialised.
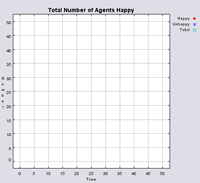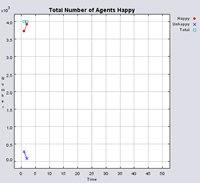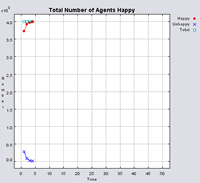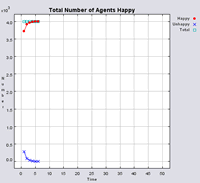
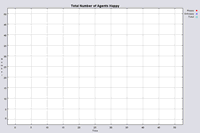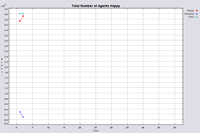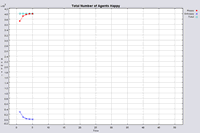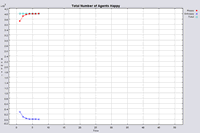
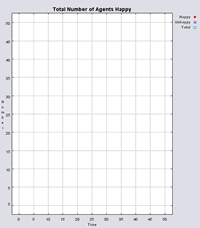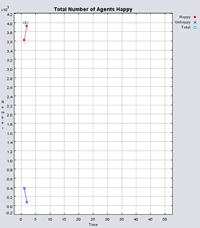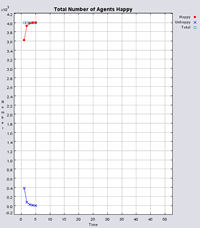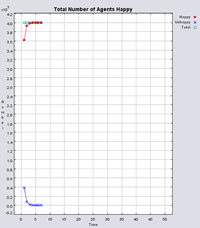
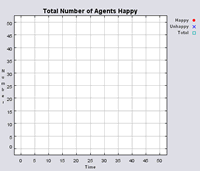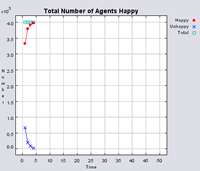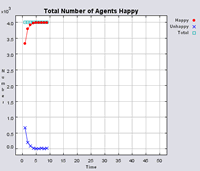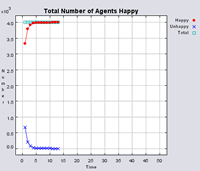
The following section will highlight multiple model runs that were carried out for a range of different density values (ranging from 2000 to 850 agents per km2). Below the 850 agents per km2 threshold, agents were removed from the system until there was enough free space for their tolerance for density to be met. Each simulation was stopped once all agents were satisfied with their neighbourhoods. Table 1 presents summary statistics for the average outcomes of multiple model runs with different density tolerances. As density increases, the total number of agents that move on average during the course of a simulation decreases.
Post analysis of the model was carried out in a GIS package to investigate whether or not the model was working correctly. This was achieved by using the final position of the agents, creating a buffer of 100m around each agent to reflect its neighbourhood and calculating how many agents fell within this buffer. Agents that fell within the search radius are summed, and then divided by the search area, to get each agents’ final population density. This is the same method as used within the model for calculating population density. The final four columns in Table 1 highlight sources of error within the model. As the density value becomes smaller, the source of error increases. This is a result of conversion factors from metres to decimal degrees in the model and between decimal degrees to metres in the GIS. None of the maximum values are above 100 people per km2 of the value set by the model, while the percentage of agents with this maximum value as a percentage of agents above set density threshold ranges from 0 to 15%. Figure 3 highlights agents where their final density is above the specified level set by the model. As density increases, the number of agents above the level decreases along with the range of values which correlates with the data shown in Table 1.
Table 1: Average (mean) results for different maximum density for 100m neighbourhoods.
Figure 3: Error and the frequency of variation with different density levels.
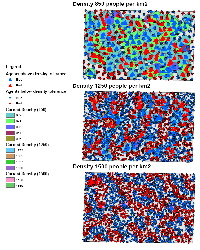
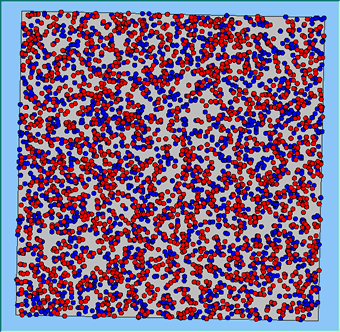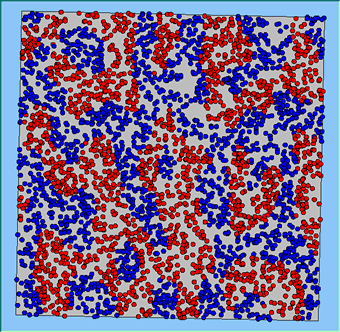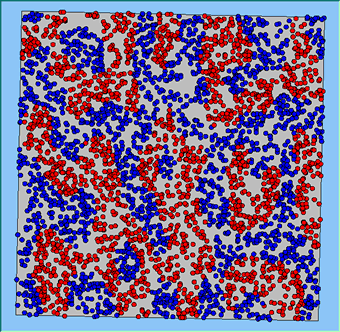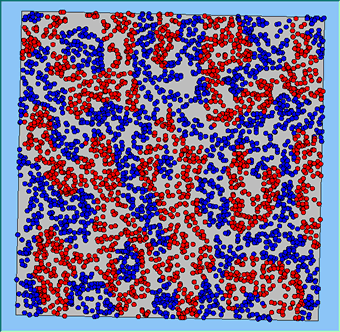
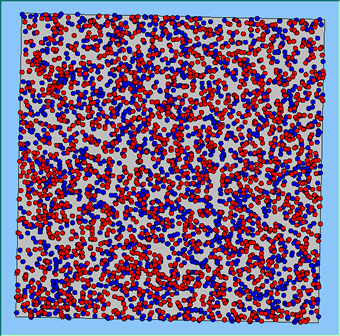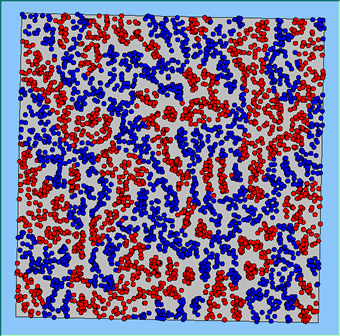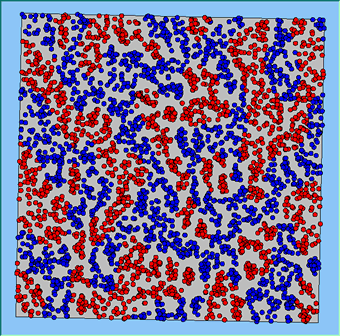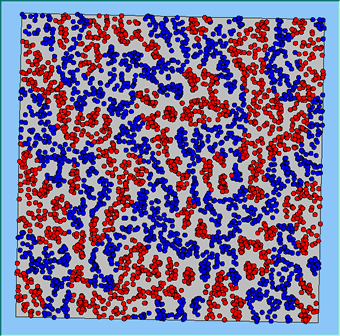
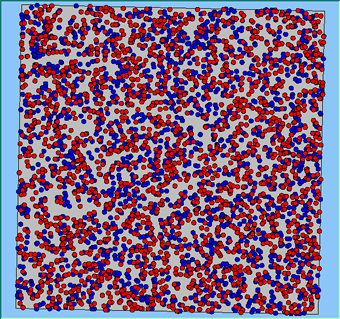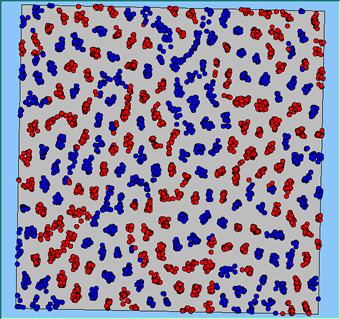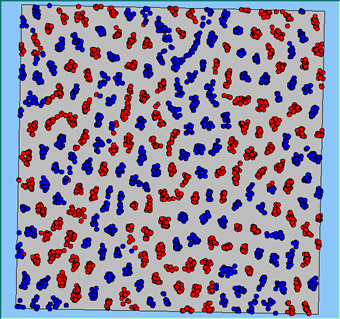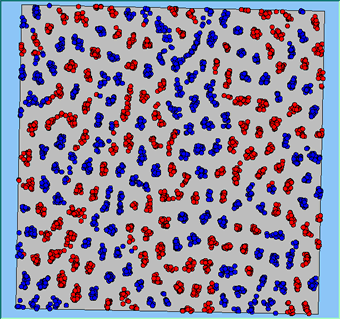
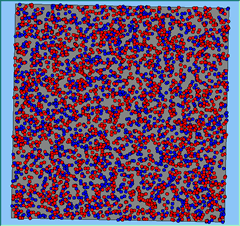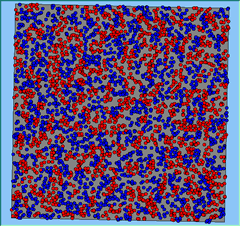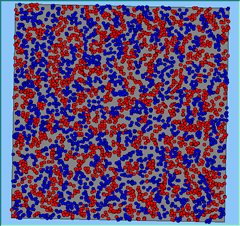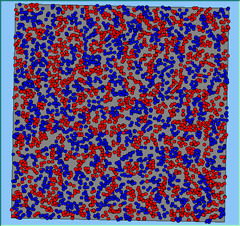
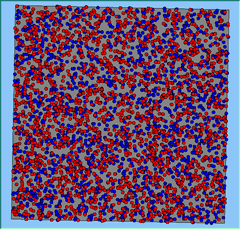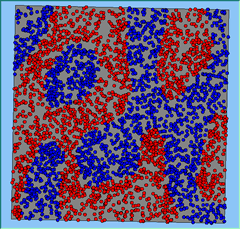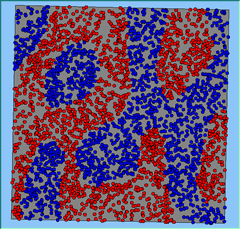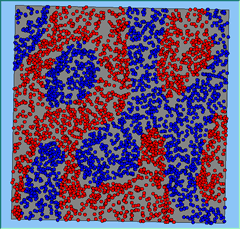
Figure 4 highlights the typical patterns that different density values have on the pattern of segregation that emerges. One thing which becomes noticeable as density values decrease is the effect that neighbourhood sizes have on the final pattern of segregation that emerges. Clusters of different groups become more distinct. Therefore the role neighbourhoods have on the final pattern of segregation was explored further. Animations of these simulation runs can be seen below.
Figure 4: Typical patterns of segregation when agents are all satisfied for different maximum density of neighbourhoods.
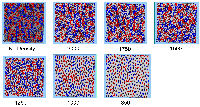
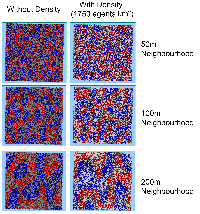
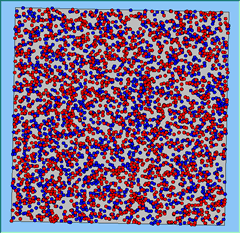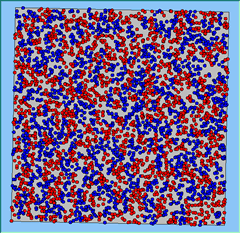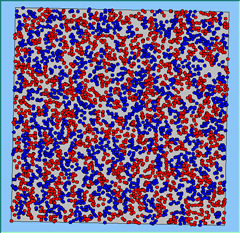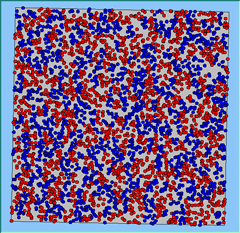
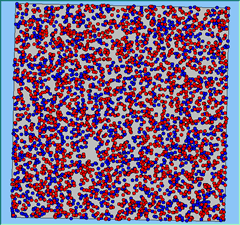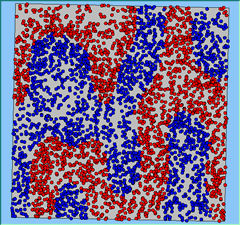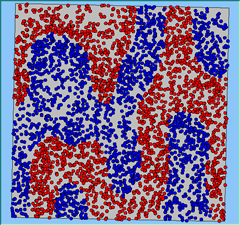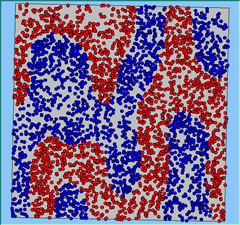
Three different neighbourhood sizes were tested, that of 50, 100 and 200m all with a density of 1750 agents per km2 (Table 2). As with other experiments, as areas become smaller the source of error increases while additionally the number of times agents move also decreases. Figure 5 demonstrates how the final pattern of segregation varies between different neighbourhood sizes and between models that use and do not use density constraints. There is little difference in the final patterns of segregation that emerge. Animations of these simulation runs can be seen below.
Table 2: Average (mean) results for different neighbourhood sizes for the same maximum density (1750 agents per km2).
Figure 5: A comparison between the patterns of segregation that emerge for different size neighbourhoods.
Typical patterns of segregation when agents are all satisfied for different maximum density of neighbourhoods.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
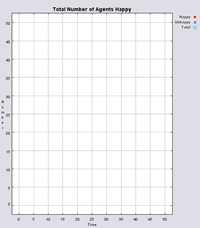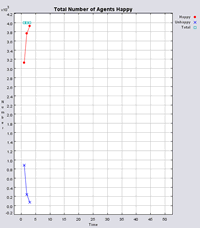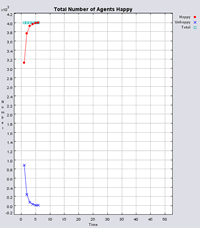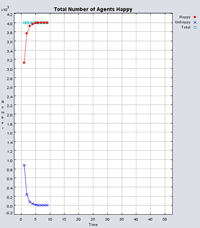 |
 |
 |
 |
|
A comparison between the patterns of segregation that emerges for different size neighbourhoods
Without Density |
With Density (1750 agents km2) |
Neighb-ourhood Size |
||
 |
 |
 |
 |
50m |
 |
 |
 |
 |
100m |
 |
 |
 |
 |
200m |