Kosko (1992) has introduced a mode of representation of fuzzy sets as points in an N-dimensional Euclidean space. This is a unit hypercube where the axes correspond to the possible membership values of the set (picture1).

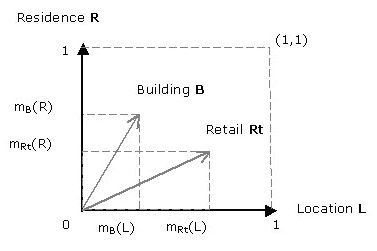
So, we can for example represent an object "building" as a point in relation to "residence" and "location". The membership functions are the coordinates of the point. In crisp logic, building B would be represented on the convexes of the 2dimensional space. The position of B in relation to location L and residence R would be absolute, 0 or 1 (picture2). In fuzzy logic we can express more intuitive perceptions about objects and their relations. The option of establishing a "building" would be an acceptable possibility if it was place a bit further from the specific location, and the function of the building could be maintained as "residence" except maybe not as 100%, since other activities will be associated with this building. We can represent another object "retail" in the same diagram. The critical issue here is to develop a method to capture the interdependency between the building B and land use Retail.

We can understand interdependencies by means of logical connectives or set relationships. And we use the subsethood theorem introduced by Kosko in order to define these connectives.

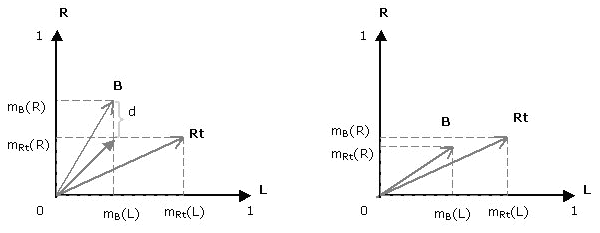
In classic fuzzy theory if B is inside the box formed by Rt, we say that B implies Rt and Rt does not imply B (B is a subset of Rt). If one dimension of B is slightly higher than Rt then B is not a full subset of Rt. The subsethood measurement suggests that by measuring the distance among fuzzy sets, we can have a measurement of the degree that B is subset of Rt and hence the degree that B implies Rt. The distance d is an indicator for the interdependency of B and Rt (picture3). In that way we capture their interdependency using their definition as fuzzy sets.

Using this representation how can we say if building B implies the land use Retail? In crisp logic an implication is valid when the set B is subset of Rt. But what if B is slightly outside the boundaries of Rt? The subsethood measurement starts with the hypothesis that a set can be partly subset and partly superset of another fuzzy set. The greater the violation the less the building B is subset of the retail Rt and the more is a superset. So, the key idea is metrical: we need to measure the Euclidean distance of B with the closest subset of Rt as illustrated in the figure (picture3).

Briefly, as logical connectives and set relationships are equivalent, the implication is evaluated on the basis of measuring the distance among fuzzy sets. This measurement indicates the degree that the building B implies Retail Rt or the opposite. In this way we capture their interdependency using their definition as fuzzy sets.